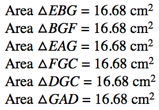Centroid of a Triangle
by Zack Kroll
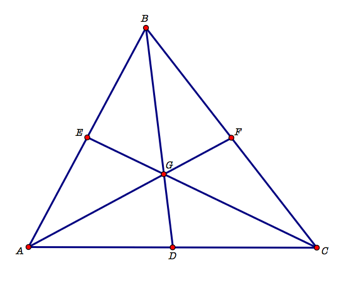
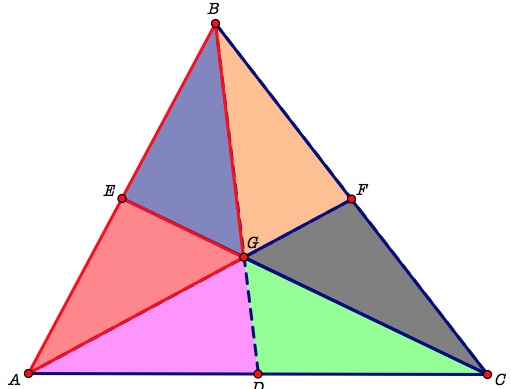
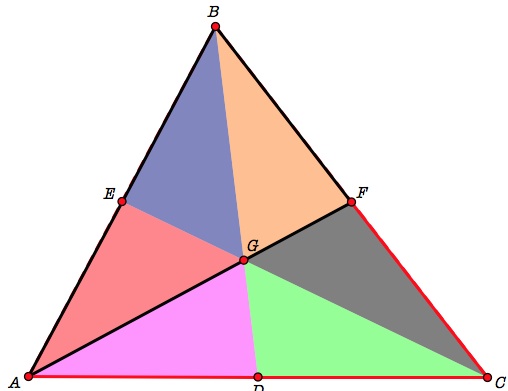
First we begin by constructing the centroid of a triangle, the concurrence of three medians. In order to find the medians we must first determine the midpoint of each of the three sides of the figure. In triangle ABC, the midpoint of AB is E, midpoint of BC is F, and the midpoint of AC is D. From there we construct segment from each midpoint to the opposite vertex. Those three line segments intersect at a single point, G, inside of the figure. This point is what we call the centroid.
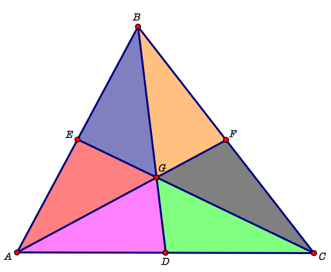
After constructing the centroid, G, of the triangle, we realize that there are six triangles inside of the ABC. The triangles appear to look congruent to one another, but we are unsure. Our goal is to determine whether all of the triangles are congruent and if so, how can we be certain. Each of the figures is color coded in order to differentiation between them.
The simplest way is by using the technology given to us. In GeometerŐs Sketchpad we calculate the area of each of the triangles. Through this we are able to determine that indeed the areas of the six triangles are equivalent. This makes us believe that finding the centroid by constructing the medians of a triangle will generate six triangles with equal areas.
Besides using the functions in GeometerŐs Sketchpad we can also show that the area of each of the six triangles is equivalent using a more mathematical approach.
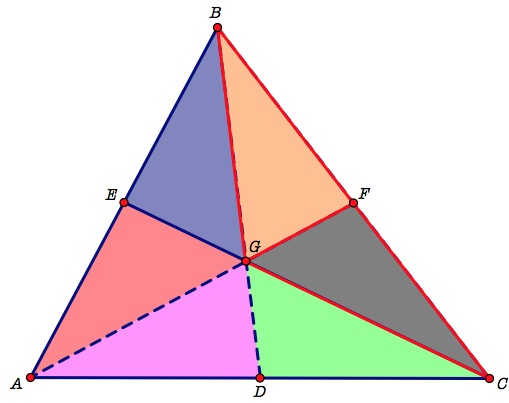
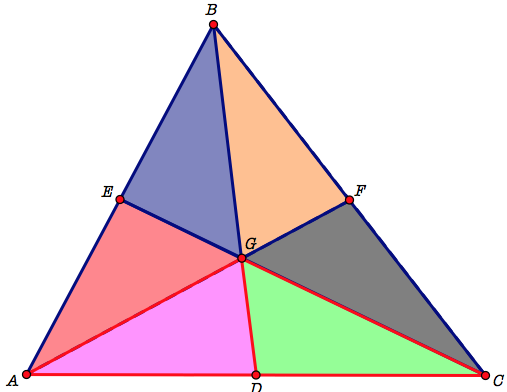
We begin this by finding the areas of two triangles: BGF and CGF. These two triangle have the same height and equal bases. The reason the bases lengths are the same is because we bisected them when finding the midpoint F. We know that triangles BGF and CGF are congruent. The next thing we turned our attention to was triangles BGE and AGE. Once again, these two figures have the same height. bases lengths because we bisected the segment AB in order to construct the median EC.The third set of two triangles is AGD and CGD. These two triangles have the same height and base lengths meaning that they have equivalent areas. The base lengths are the same because we bisected the side AC when we constructed the median BD.
From there we can look at the two triangles formed on either
side of each of the three medians.
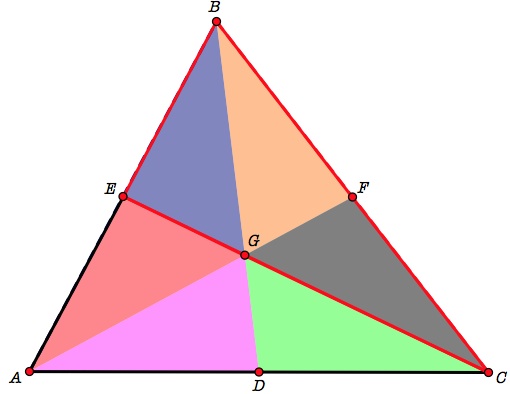
We have determined that there are three sets of two triangles with each pair having congruent areas. This does not tell us how those triangles relate to the other four. However we can apply similar logic to these sets of two as we did with the others in the previous examples. Triangles BCE and ACE are congruent because they have the same height and equal bases. The base of each of the two triangles is half of the segment AB, where E is the midpoint.
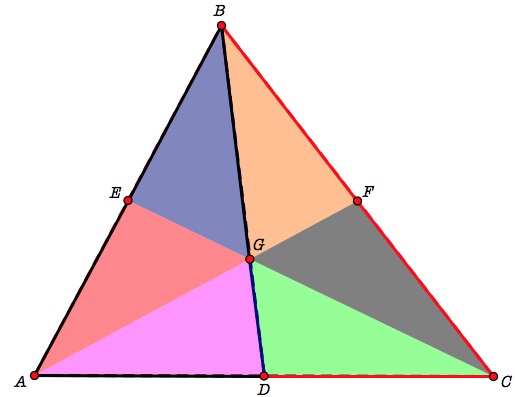
Using this reasoning we can comfortably say that triangles ABD and CBD are congruent as well as triangles BAF and CAF.
Through this process we are certain that the six triangles formed by finding the centroid of a triangle are all congruent.